This is an informal lectures series on the introduction to the mathematical formulation of the geometric and stochastic quantizations, also on some current development and related topics.
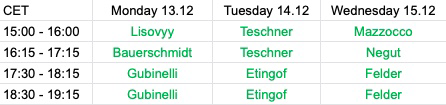
Time:Mon-Wed, December 13-15, 2021
3 pm-7 pm Central Europe Time
(6-10 am PST, 9 am-1 pm EST, 4 pm-8 pm Finland)
Speaker list:
Roland Bauerschmidt (Cambridge)
Pavel Etingof (MIT)
Giovanni Felder (ETH Zürich)
Massimiliano Gubinelli (Bonn)
Oleg Lisovyy (Tours)
Marta Mazzocco (Birmingham)
Andrei Negut (MIT)
Jörg Teschner (University of Hamburg and DESY)
Schedule in CET (-9=PST, -6=EST)
The zoom invitation will be distributed through the email list a few days prior to the lectures. You can contact Promit ([email protected]) to be added to the mailing list. You may also share it with your colleagues and students, but please do not post it on a publicly viewable website.
Organizers:
Promit Ghosal (MIT, [email protected])
Eveliina Peltola (Bonn & Aalto, [email protected])
Gabriele Rembado (Bonn, [email protected])
Yilin Wang (MIT, [email protected])
Organizers:
Promit Ghosal (MIT, [email protected])
Eveliina Peltola (Bonn & Aalto, [email protected])
Gabriele Rembado (Bonn, [email protected])
Yilin Wang (MIT, [email protected])
Abstract
Roland Bauerschmidt (Cambridge)
Nonlinear sigma models (and applications to random forests)
I will explain what nonlinear sigma models are, why they are interesting, and what is mathematically understood. I will then present results about the nonlinear sigma model with
OSp(1|2) symmetry which is exactly related to the probabilistic model of random forests.
Pavel Etingof (MIT)
Introduction to the analytic Langlands correspondence
I will review an analytic approach to the geometric Langlands correspondence, following my work with E. Frenkel and D. Kazhdan, arXiv:1908.09677, arXiv:2103.01509, arXiv:2106.05243. This approach was developed by us in the last couple of years and involves ideas from previous and ongoing works of a number of mathematicians and mathematical physicists -- Kontsevich, Langlands, Nekrasov, Teschner, Gaiotto-Witten and others. One of the goals of this approach is to understand single-valued real analytic eigenfunctions of the quantum Hitchin integrable system. The main method of studying these functions is realizing them as the eigenbasis for certain compact normal commuting integral operators the Hilbert space of L2 half-densities on the (complex points of) the moduli space Bun(G,X) of principal G-bundles on a smooth projective curve X, possibly with parabolic points. These
operators actually make sense over any local field, and over
non-archimedian fields are a replacement for the quantum Hitchin system. We conjecture them to be compact and prove this conjecture in the genus zero case (with parabolic points) for G=PGL(2).
I will first discuss the simplest non-trivial example of Hecke operators over local fields, namely G=PGL(2) and genus 0 curve with 4 parabolic points. In this case the moduli space of semistable bundles Bun(G,X)^{ss} is P^1, and the situation is relatively well understood; over C it is the theory of single-valued eigenfunctions of the Lame operator with coupling parameter -1/2 (previously studied by Beukers and later in a more functional-analytic sense in our work with Frenkel and Kazhdan). I will consider the corresponding spectral theory and then explain its generalization to N>4 points and conjecturally to higher genus curves.
Giovanni Felder (ETH Zürich)
Dynamical quantum groups in statistical mechanics
In the first part I will review the theory of the Yang-Baxter equation and the appearance of quantum groups in statistical mechanics and quantum integrable systems. In the second part I will concentrate on the case of solid-on-solid models and report on joint work with Muze Ren on the related representations of dynamical quantum groups on groupoid-graded vector spaces.
Massimiliano Gubinelli (Bonn)
Some aspects of stochastic quantisation
I will give a general perspective on stochastic quantization as a method to construct euclidean quantum field theories by stressing the general ideas, the techniques and the open problems. The aim is to show how stochastic quantization can be implemented in many different but analogous ways which hint to an underlying basic structure, still not well understood.
Oleg Lisovyy (Tours)
Accessory parameters in Heun equations and classical conformal
blocks
I will start by discussing a conjecture of Zamolodchikov which relates quasiclassical conformal blocks of the Virasoro algebra and accessory parameters of Floquet type in Heun equations. Then I will explain a construction of several types of irregular conformal blocks. Finally, I will propose an extension of the conjecture to another class of accessory parameter functions that are defined by inverting all-order Bohr-Sommerfeld periods for the confluent and biconfluent Heun equation.
Marta Mazzocco (Birmingham)
Isomonodromic deformations: Confluence, Reduction, Quantisation
In this talk I will describe the isomonodromic deformations of systems of differential equations with poles of any order on the Riemann sphere as Hamiltonian flows on the product of co-adjoint orbits of the Takiff algebra (i.e. truncated current algebra). Our motivation is to produce confluent versions of the celebrated Knizhnik--Zamolodchikov equations and explain how their quasiclassical solution can be expressed via the isomonodromic tau-function. In order to achieve this, we study the confluence cascade of r+ 1 simple poles to give rise to a singularity of arbitrary Poincaré rank r as a Poisson morphism and explicitly compute the isomonodromic Hamiltonians.
Andrei Negut (MIT)
Quivers and quantum loop groups
Shuffle algebras give useful presentations of quantum groups. I will survey recent developments of a particular type of shuffle algebra (which originated in the work of Feigin-Odesskii) that one may use to define a quantum loop group for any quiver. Time permitting, I may discuss applications to the study of K-theoretic Hall algebras of quivers and surfaces, as well as Hall algebras of categories of coherent sheaves on algebraic curves over F_q.
Jörg Teschner (University of Hamburg and DESY)
Noncompact WZW models, Liouville theory, and geometric Langlands correspondence
In the first part of my talk I'll introduce to conformal field theories with affine Lie algebra symmetry in a way that provides a bridge between the field theoretical perspective which puts the focus on correlation functions and the differential equations satisfied by them on the one side to the alternative formulation based on representation theory of affine Lie algebras and the complex analysis of Riemann surfaces on the other side. Specialising to affine Lie algebras at the critical level I'll outline the relation to the CFT-based approach to the geometric Langlands correspondence pioneered by Beilinson and Drinfeld.
My goal for the second part is to describe a relation between correlation functions of a noncompact WZW model and Liouville theory related to an extension of the geometric Langlands correspondence deforming the correspondence studied by Beilinson and Drinfeld away from the critical level. It will be pointed out that the recent advances in the probabilistic approach to Liouville theory can be used to rigorously construct correlation functions of the corresponding noncompact WZW model, the WZW model associated to the hyperbolic three-dimensional space H_3. The theory obtained in this way can be regarded as a quantum version of the analytic Langlands correspondence recently studied by Etingof, Frenkel and Kazhdan.
Nonlinear sigma models (and applications to random forests)
I will explain what nonlinear sigma models are, why they are interesting, and what is mathematically understood. I will then present results about the nonlinear sigma model with
OSp(1|2) symmetry which is exactly related to the probabilistic model of random forests.
Pavel Etingof (MIT)
Introduction to the analytic Langlands correspondence
I will review an analytic approach to the geometric Langlands correspondence, following my work with E. Frenkel and D. Kazhdan, arXiv:1908.09677, arXiv:2103.01509, arXiv:2106.05243. This approach was developed by us in the last couple of years and involves ideas from previous and ongoing works of a number of mathematicians and mathematical physicists -- Kontsevich, Langlands, Nekrasov, Teschner, Gaiotto-Witten and others. One of the goals of this approach is to understand single-valued real analytic eigenfunctions of the quantum Hitchin integrable system. The main method of studying these functions is realizing them as the eigenbasis for certain compact normal commuting integral operators the Hilbert space of L2 half-densities on the (complex points of) the moduli space Bun(G,X) of principal G-bundles on a smooth projective curve X, possibly with parabolic points. These
operators actually make sense over any local field, and over
non-archimedian fields are a replacement for the quantum Hitchin system. We conjecture them to be compact and prove this conjecture in the genus zero case (with parabolic points) for G=PGL(2).
I will first discuss the simplest non-trivial example of Hecke operators over local fields, namely G=PGL(2) and genus 0 curve with 4 parabolic points. In this case the moduli space of semistable bundles Bun(G,X)^{ss} is P^1, and the situation is relatively well understood; over C it is the theory of single-valued eigenfunctions of the Lame operator with coupling parameter -1/2 (previously studied by Beukers and later in a more functional-analytic sense in our work with Frenkel and Kazhdan). I will consider the corresponding spectral theory and then explain its generalization to N>4 points and conjecturally to higher genus curves.
Giovanni Felder (ETH Zürich)
Dynamical quantum groups in statistical mechanics
In the first part I will review the theory of the Yang-Baxter equation and the appearance of quantum groups in statistical mechanics and quantum integrable systems. In the second part I will concentrate on the case of solid-on-solid models and report on joint work with Muze Ren on the related representations of dynamical quantum groups on groupoid-graded vector spaces.
Massimiliano Gubinelli (Bonn)
Some aspects of stochastic quantisation
I will give a general perspective on stochastic quantization as a method to construct euclidean quantum field theories by stressing the general ideas, the techniques and the open problems. The aim is to show how stochastic quantization can be implemented in many different but analogous ways which hint to an underlying basic structure, still not well understood.
Oleg Lisovyy (Tours)
Accessory parameters in Heun equations and classical conformal
blocks
I will start by discussing a conjecture of Zamolodchikov which relates quasiclassical conformal blocks of the Virasoro algebra and accessory parameters of Floquet type in Heun equations. Then I will explain a construction of several types of irregular conformal blocks. Finally, I will propose an extension of the conjecture to another class of accessory parameter functions that are defined by inverting all-order Bohr-Sommerfeld periods for the confluent and biconfluent Heun equation.
Marta Mazzocco (Birmingham)
Isomonodromic deformations: Confluence, Reduction, Quantisation
In this talk I will describe the isomonodromic deformations of systems of differential equations with poles of any order on the Riemann sphere as Hamiltonian flows on the product of co-adjoint orbits of the Takiff algebra (i.e. truncated current algebra). Our motivation is to produce confluent versions of the celebrated Knizhnik--Zamolodchikov equations and explain how their quasiclassical solution can be expressed via the isomonodromic tau-function. In order to achieve this, we study the confluence cascade of r+ 1 simple poles to give rise to a singularity of arbitrary Poincaré rank r as a Poisson morphism and explicitly compute the isomonodromic Hamiltonians.
Andrei Negut (MIT)
Quivers and quantum loop groups
Shuffle algebras give useful presentations of quantum groups. I will survey recent developments of a particular type of shuffle algebra (which originated in the work of Feigin-Odesskii) that one may use to define a quantum loop group for any quiver. Time permitting, I may discuss applications to the study of K-theoretic Hall algebras of quivers and surfaces, as well as Hall algebras of categories of coherent sheaves on algebraic curves over F_q.
Jörg Teschner (University of Hamburg and DESY)
Noncompact WZW models, Liouville theory, and geometric Langlands correspondence
In the first part of my talk I'll introduce to conformal field theories with affine Lie algebra symmetry in a way that provides a bridge between the field theoretical perspective which puts the focus on correlation functions and the differential equations satisfied by them on the one side to the alternative formulation based on representation theory of affine Lie algebras and the complex analysis of Riemann surfaces on the other side. Specialising to affine Lie algebras at the critical level I'll outline the relation to the CFT-based approach to the geometric Langlands correspondence pioneered by Beilinson and Drinfeld.
My goal for the second part is to describe a relation between correlation functions of a noncompact WZW model and Liouville theory related to an extension of the geometric Langlands correspondence deforming the correspondence studied by Beilinson and Drinfeld away from the critical level. It will be pointed out that the recent advances in the probabilistic approach to Liouville theory can be used to rigorously construct correlation functions of the corresponding noncompact WZW model, the WZW model associated to the hyperbolic three-dimensional space H_3. The theory obtained in this way can be regarded as a quantum version of the analytic Langlands correspondence recently studied by Etingof, Frenkel and Kazhdan.